Abstract
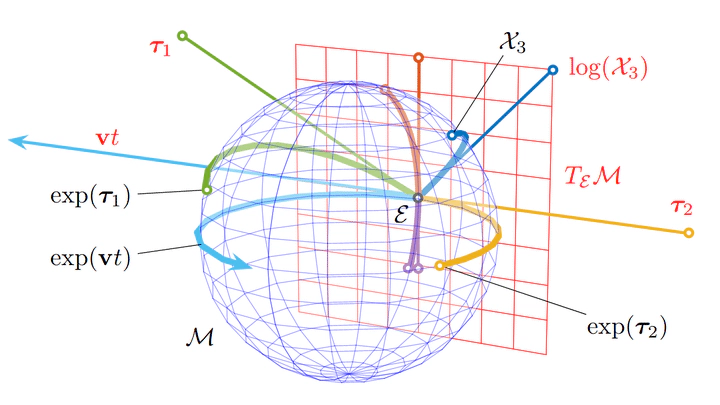
In this work, we investigate the SO(3) logarithmic map from various points of view. First, we propose two numerically stable solutions to the degenerate case of the logarithmic map (from SO(3) rotation matrices to so(3)-Lie algebra vectors) when the angle of rotation is close to or exactly pi. Second, we observe and theoretically prove that the Jacobian of the logarithmic map in a manifold sense (as the linear map between tangent spaces) can be found as a chain of Jacobians in a numerical sense of the logarithmic map and box plus operator via extending logarithmic map over the SO(3) manifold. Moreover, we show that the result of the chain rule does not depend on the extension of the log map, even though the numerical Jacobians of different extensions are different. These results ensure that we do not run into degenerate cases in practical implementations of optimization algorithms, such as with the Ceres solver library, for applications like pose graph optimization. We have proposed corresponding improvements to the implementation of SO3 in the popular Sophus library